Получено первое трехмерное изображение множества Мандельброта
Рекурсивные фигуры генерируются в соответствии с "итеративной" процедурой: Вы применяете уравнение к числу, применяете то же самое уравнение к результату и повторяете этот процесс много раз. Когда результаты представляются в геометрической формуле, они могут производить поразительные "самоподобные" изображения, формы, которые содержат те же самые формы в различных масштабах; например, некоторые странно походят на снежинку. Наиболее хитрой частью является нахождение уравнения, которое произведет интересное изображение.
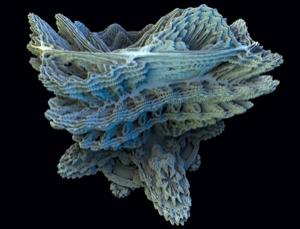
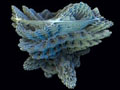
(Первое изображение множества Мандельброта - бесконечно самоповторяющейся фигуры)
Самое известное рекурсивное уравнение - двухмерное множество Мандельброта, названное в честь математика Бенуа Мандельброа из Йельского Университета, который придумал название "Фракталы" для получающихся форм в 1975.
Есть и много других типов рекурсивных уравнений, в том числе и в трех измерениях. К примеру, "Губка Менгера" является одним из самых простых трехмерных представлений.
"Уже совершались попытки трехмерного представления Мандельброта, но они не отображали реальное рекурсивное поведение", говорит Дэниел Вайт, исследователь фракталов из Бедфорда, Великобритания. "Наше изображение - первое полноценное трехмерное представление данного фрактала, что бесконечно самоповторяется."
Комментарии:
jenovaЭто может быть похожим на часть виртуозного вязания, но изготовители изображения, которое они называют Mandelbulb (см. изображение) утверждают, что это - самое точное трехмерное представление известнейшего рекурсивного уравнения: множества Мандельброта.
Это ж надо было так исковеркать русский язык.
Цветы: как они влияют на нашу жизнь и эмоции
Цветы играют особую роль в жизни каждого человека.
Техника Lenovo: надежность и долговечность при эксплуатации
Покупка технического устройства - это процесс, в котором важно учитывать различные нюансы, напрямую связанные с базовыми характеристиками приспособления и его функциональностью.
Лучшие модели наушников JBL: обзор и характеристики
JBL наушники широко известны высоким качеством звука и надёжностью, благодаря чему они завоевали доверие различных категорий пользователей — от меломанов до спортсменов.
Причины роста популярности Астрономии и Космоса среди молодого поколения
Астрономия и космос всегда привлекали внимание людей всех возрастов, но особенно ярко эта наука проявляется среди молодого поколения.
Техника Lenovo: надежность и долговечность при эксплуатации
Покупка технического устройства - это процесс, в котором важно учитывать различные нюансы, напрямую связанные с базовыми характеристиками приспособления и его функциональностью.
Лучшие модели наушников JBL: обзор и характеристики
JBL наушники широко известны высоким качеством звука и надёжностью, благодаря чему они завоевали доверие различных категорий пользователей — от меломанов до спортсменов.
e-Learning в цифрах: 6 общих фактов, много данных и прогнозы на ближайшее будущее
e-Learning – это обучение с помощью цифровых технологий (Интернета, электронных устройств и специальных программ). Процесс можно организовать в аудиториях или удалённо, одновременно для целой группы или по гибкому графику для каждого.
Компьютерный чип со встроенной тканью человеческого мозга получает финансирование от военных
В прошлом году ученые из Университета Монаша создали «DishBrain» — полубиологический компьютерный чип, в электродах которого в лаборатории выращено около 800 000 клеток мозга человека и мыши. Демонстрируя что-то вроде разума, он научился играть в пинг-понг за 5 минут.
